Introduction
Adaptive mesh refinement (AMR) applications to solve partial differential equations (PDE) are very challenging to scale efficiently to the petascale regime. For the next major release of Chombo, we have been able to use metadata compression to allow us to weakly scale both hyperbolic and elliptic applications to 100K processors.That we are able to achieve petascale performance without distribution of the metadata is a significant advance which allows for much simpler and faster AMR codes.
Replication Scaling
With replication scaling, we take a grid hierarchy and data for a fixed number of processors and scale it to higher concurrencies by making identical copies of the hierarchy and the data. Replication scaling tests most aspects of weak scalability, is simple to define, and provides results that are easy to interpret. Thus it is a very useful tool for understanding and correcting impediments to efficient scaling in an AMR context. Below is an example of before and after a 2x2 replication. Each little cube is a 16^3 grid.
|
|
Optimizations
To achieve our performance results for the two 3D Chombo applications discussed, several important changes were made to the standard code.A run-length compression method was used to greatly reduce the memory overhead associated with the metadata for the grids. There were also application-specific optimizations. For example, for our hyperbolic application, we optimized inter-level coarse-fine interpolation objects to take advantage of our new metadata structure. For our elliptic solver, we carefully control the number of communication steps necessary and greatly reduce the number of all-to-all communications in the multigrid algorithm for AMR.
Memory
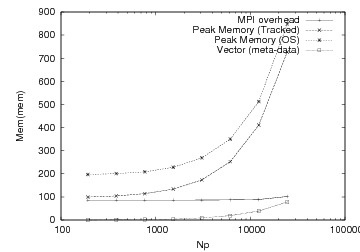
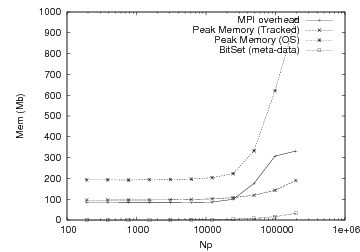
These graphs show the improvement of memory performance for a hyperbolic problem. Our optimizations allowed us to run an order of magnitude larger problem.
|
Before Optimizations |
|
After Optimizations |
|
|
|
|
|
|
|---|
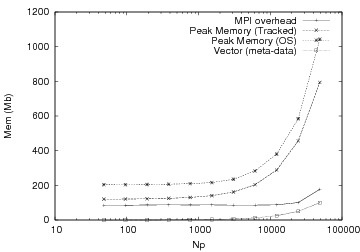
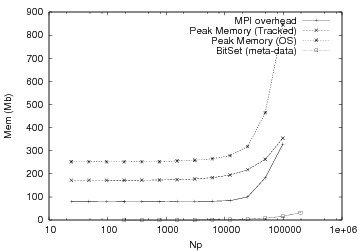
These graphs show the improvement of memory performance for an elliptic problem. Our optimizations allowed us to run an order of magnitude larger problem.
|
Before Optimizations |
After Optimizations |
|
|
|
|---|
Run Time
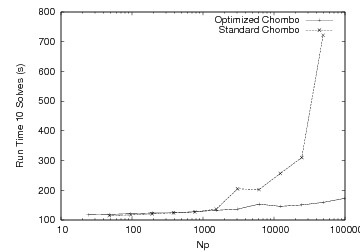
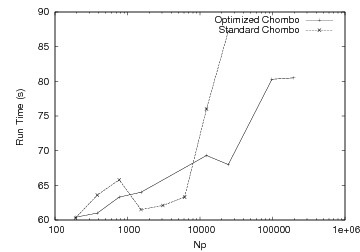
These graphs show comparisons in runtime performance for elliptic and hyperbolic applications. We show good weak scaling in both cases.
|
Elliptic Application |
Hyperbolic Application |
|
|
|
|---|
Full Paper
The full submission is given here: paper